Le milieu des probabilités
Les contraintes pour construire les grands modèles de langage, comme ChatGPT, sont de différents ordres. Essayons dans cet article d’aborder une contrainte fondamentale et hors du champ humain, les mathématiques, en particulier les probabilités qui sont au cœur de ces objets techniques.
Les probabilités désignent l’étude des phénomènes aléatoires, par exemple les résultats possibles d’un lancer de dés. Sa compréhension permet, entre autres, de prédire comment des phénomènes aléatoires distincts se combinent et ce qu’ils produisent. Quelles sont les probabilités d’avoir un six, si nous lançons deux, trois ou quatre dès ? Quelle est la probabilité d’avoir telle ou telle maladie étant donné le contexte génétique et environnemental ? En effet, les probabilités ne se mélangent pas « n’importe comment », elles suivent les rigides contraintes des mathématiques.
Une loi mathématique incontournable pour comprendre comment les probabilités s’additionnent est le Théorème Central Limite qui dit que le type de probabilité produite par une somme de phénomènes aléatoires finira toujours par avoir la même forme, une « Gaussienne » ou loi normale.
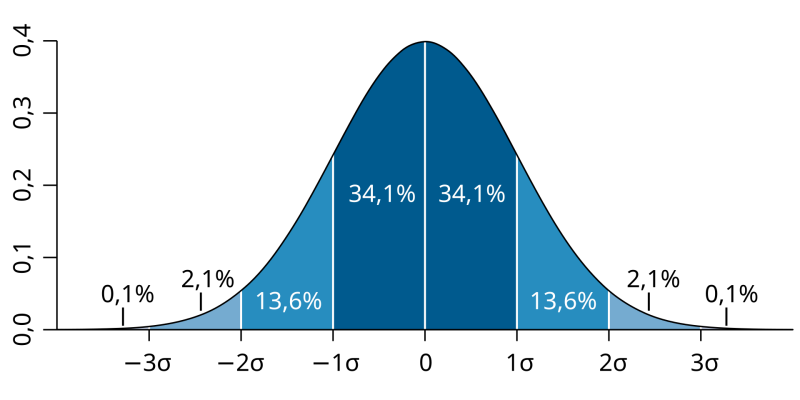
Source : https://commons.wikimedia.org/wiki/File:Standard_deviation_diagram_(decimal_comma).svg
Cette forme représente comment les événements aléatoires se répartissent dans les différents résultats que ces événements peuvent prendre : plus la courbe est haute, plus l’événement est probable. Elle est caractérisée par sa courbure et sa symétrie ; les éléments les plus probables se trouvent au centre, la moyenne, et ceux plus rares dans les « queues » de la courbe. Prenons un exemple : la taille des femmes. Si nous mesurons la taille d’un nombre relativement important de personnes, nous allons obtenir une répartition des mesures similaire à une gaussienne. La moyenne en Belgique sera aux alentours de 164 cm, au centre de la courbe. La plupart des personnes se trouveront aux alentours, mais au plus nous nous éloignerons de la moyenne, au plus il sera rare de trouver une personne faisant cette taille.
Pourquoi est-ce important et comment cela contraint-il le milieu technique ? Parce qu’un technicien qui travaille avec de l’aléatoire aimerait parfois avoir une courbe plutôt asymétrique, c’est-à-dire que les déviations de sa machine soit plutôt d’un côté que d’un autre, par exemple si un côté est plus dangereux . Or il n’a pas le choix dans la forme des probabilités. Il ne peut agir que sur les phénomènes aléatoires sous-jacents à sa machine et ainsi chercher à réduire le hasard.
Dans les grands modèles de langage
Une des hypothèses des grands modèles de langage est de dire que le langage a un caractère probabiliste. C’est-à-dire que l’écriture d’un texte peut prendre plusieurs formes tout en gardant la même signification, il y a juste des manières plus probables que d’autres. Parfois l’ensemble des mots peut varier, parfois seulement certains si l’on veut garder le sens du texte.
En particulier, lorsqu’un grand modèle de langage veut prédire le mot suivant d’un texte, il ne prend pas le mot le plus probable, mais un ensemble de mot probable et va choisir, au hasard, un des mots pour constituer sa phrase. Ceci est mis en place pour que le texte paraisse plus « naturel ». Chaque LLM paramètre finement ce hasard : au plus le mot sera choisi au hasard, au plus le texte sera « créatif », mais au risque de dénaturer le sens, voire de produire quelque chose qui ne veut plus rien dire comme dans le cas des hallucinations.